好像有式子爆炸了,所以还是推荐一下去luogu博客看(卑微)
题面描述
给出一棵树,告诉你每条边对答案的贡献为边两边联通块大小差的绝对值乘上边权,让你求出所有边的贡献之和。
如果没有听懂的话也可以继续看下面的分析。
分析
样例是这样的一颗树
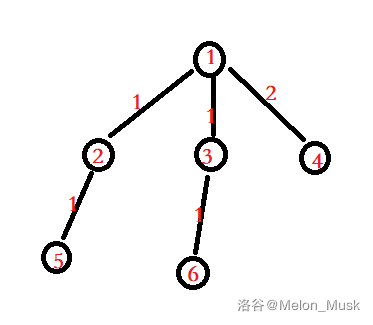
可以手推一下这个例子让你更清楚的理解题意。
由于考虑每条边上的贡献仅由边权和边两边的联通块大小确定,而我们只要知道任意一边的联通块的大小,通过 n-联通块大小 即可得知另一块连通块地大小。
所以我们使用$size_i$记录以i为根的子树的大小,那么一条边上的贡献就是
$$dist_{i,j}|size[i]-(n-size[i])|=dist_{i,j}|size[i]*2-n|$$
直接用dfs求解即可
完整代码
直接按分析简单模拟即可。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=10000010;
ll n,cnt,ans;
ll size[maxn],head[maxn];
struct node
{
int w,to,nt;
}e[maxn*2];
void add(int x,int y,int z)
{
cnt++;
e[cnt].to=y;
e[cnt].nt=head[x];
e[cnt].w=z;
head[x]=cnt;
}
void dfs(int x,int fa)
{
size[x]=1;
for(int i=head[x];i;i=e[i].nt)
{
int to=e[i].to;
if(fa==to) continue;
dfs(to,x);
size[x]+=size[to];
ans+=e[i].w*abs(2*size[to]-n);
}
}
int main()
{
cin>>n;
for(int i=1;i<n;i++)
{
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
add(x,y,z);
add(y,x,z);
}
dfs(1,0);
cout<<ans<<endl;
return 0;
}
0 条评论