CF626C Block Towers

CF626C Block Towers 题面

写完发现这题题解里没有我的做法，感觉这个做法更简单实用，故分享给大家。

分析

因为每个人的塔的高度要不相同，假设只有 2 层 2 层往上搭的话，那么很显然每个人只要都比前面的人多搭 2 层即可，所以n个人搭的高度为 2 * n 。

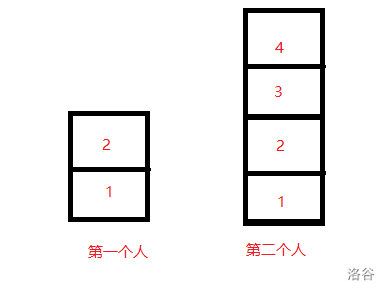
只有 3 层往上搭的同理，高度为 3 * m。

我们记 n 个 2 层 2 层往上搭的人的总高度为 sum1 ， m 个 3 层 3 层往上搭的人的总高度为 sum2 。

所以一开始我们先令 sum1 = 2 * n , sum2 = 3 * m。

而本题同时有 2 层搭的和 3 层搭的，此时我们注意到，当第三个搭 2 层的人和第二个搭3层的人的高度均为 6 。

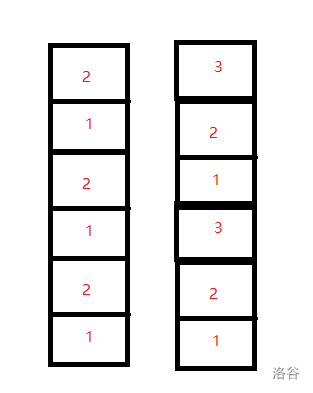
所以此时，我们应该把其中一个人让他再叠 2 层或 3 层使两人高度不再重合。

而当一个人又叠了一次之后，他之后的所有人都得往上再叠一次，所以可以理解为 sum1 的值增加了 2 或者 sum2 的值增加了 3。为了使结果最小，我们当然会增加当前值较小的一个使总结果更小。

而当层数是 6 的倍数时，就会有这样的一次重合，本题数据告诉我们可以暴力枚举。

本题的答案为 min ( sum1 , sum2 ) 。

参考代码

#include<bits/stdc++.h> 
using namespace std;
int n,m,sum1,sum2;
int main()
{
    scanf("%d%d",&n,&m);
    sum1=n*2;sum2=m*3;
    while(n>=3 && m>=2)
    {
        if(sum1+2<=sum2+3) sum1+=2,n++;   //注意这里我们把sum1的层数加了1次，所以要n++!
        else sum2+=3,m++;
        n-=3,m-=2;
    }
    printf("%d\n",max(sum1,sum2));
    return 0;
}